Measures¶
Default measures¶
Let’s quickly create a cube from a CSV file. You can see the value of your measures at the top level of the cube by calling cube.query():
[1]:
import atoti as tt
session = tt.create_session()
store = session.read_csv("data/example.csv", keys=["ID"], store_name="First")
cube = session.create_cube(store, "FirstCube")
lvl = cube.levels
m = cube.measures
hier = cube.hierarchies
cube.query()
Welcome to atoti 0.4.0!
By using this community edition, you agree with the license available at https://www.atoti.io/eula.
Browse the official documentation at https://docs.atoti.io.
Join the community at https://www.atoti.io/register.
You can hide this message by setting the ATOTI_HIDE_EULA_MESSAGE environment variable to True.
[1]:
| Price.MEAN | Price.SUM | Quantity.MEAN | Quantity.SUM | contributors.COUNT | |
|---|---|---|---|---|---|
| 0 | 428.0 | 4280.0 | 2270.0 | 22700.0 | 10 |
SUM and MEAN aggregations are automatically created for numeric columns.
Calling cube.query() will display the value of the measure at the top level. It’s also possible to specify levels to split the cube:
[2]:
cube.query(m["Quantity.SUM"], levels=[lvl["Continent"], lvl["Country"]])
[2]:
| Quantity.SUM | ||
|---|---|---|
| Continent | Country | |
| Asia | China | 6000.0 |
| India | 3700.0 | |
| Europe | France | 7500.0 |
| UK | 5500.0 |
You can also filter on levels:
[3]:
cube.query(
m["Quantity.SUM"],
levels=[lvl["Continent"], lvl["Country"]],
condition=(lvl["Country"] == "France"),
)
[3]:
| Quantity.SUM | ||
|---|---|---|
| Continent | Country | |
| Europe | France | 7500.0 |
Aggregation functions¶
The available aggregation functions are:
[4]:
from inspect import getmembers, isfunction
[member[0] for member in getmembers(tt.agg) if isfunction(member[1])]
[4]:
['_agg',
'_count',
'_vector',
'array_quantile',
'check_literal',
'count_distinct',
'doc',
'long',
'max',
'max_member',
'mean',
'median',
'min',
'min_member',
'prod',
'quantile',
'short',
'single_value',
'sqrt',
'square_sum',
'std',
'stop',
'sum',
'var']
[5]:
m["Quantity.MIN"] = tt.agg.min(store["Quantity"])
m["Quantity.MAX"] = tt.agg.max(store["Quantity"])
m["Quantity.LONG"] = tt.agg.long(store["Quantity"])
m["Quantity.SHORT"] = tt.agg.short(store["Quantity"])
cube.query(levels=[lvl["Country"]])
[5]:
| Price.MEAN | Price.SUM | Quantity.LONG | Quantity.MAX | Quantity.MEAN | Quantity.MIN | Quantity.SHORT | Quantity.SUM | contributors.COUNT | |
|---|---|---|---|---|---|---|---|---|---|
| Country | |||||||||
| China | 380.0 | 760.0 | 6000.0 | 4000.0 | 3000.0 | 2000.0 | 0.0 | 6000.0 | 2 |
| France | 450.0 | 1800.0 | 7500.0 | 3000.0 | 1875.0 | 1000.0 | 0.0 | 7500.0 | 4 |
| India | 380.0 | 760.0 | 3700.0 | 2200.0 | 1850.0 | 1500.0 | 0.0 | 3700.0 | 2 |
| UK | 480.0 | 960.0 | 5500.0 | 3000.0 | 2750.0 | 2500.0 | 0.0 | 5500.0 | 2 |
[6]:
m["Quantity running sum"] = tt.agg.sum(
m["Quantity.SUM"], scope=tt.scope.cumulative(lvl["ID"])
)
cube.query(m["Quantity running sum"], levels=[lvl["ID"]])
[6]:
| Quantity running sum | |
|---|---|
| ID | |
| 1 | 1000.0 |
| 2 | 3000.0 |
| 3 | 6000.0 |
| 4 | 7500.0 |
| 5 | 10500.0 |
| 6 | 13000.0 |
| 7 | 15000.0 |
| 8 | 19000.0 |
| 9 | 21200.0 |
| 10 | 22700.0 |
[7]:
m["Distinct City"] = tt.agg.count_distinct(store["City"])
[8]:
m["Quantile 95"] = tt.agg.quantile(store["Quantity"], 0.95)
m["Quantile 20"] = tt.agg.quantile(store["Quantity"], 0.20)
cube.query(m["Quantile 95"], m["Quantile 20"], levels=[lvl["Continent"]])
[8]:
| Quantile 95 | Quantile 20 | |
|---|---|---|
| Continent | ||
| Asia | 3730.0 | 1800.0 |
| Europe | 3000.0 | 1500.0 |
Statistics aggregations
[9]:
m["Quantity variance"] = tt.agg.var(store["Quantity"], mode="sample")
m["Quantity standard deviation"] = tt.agg.std(store["Quantity"], mode="sample")
cube.query(m["Quantity variance"], m["Quantity standard deviation"])
[9]:
| Quantity variance | Quantity standard deviation | |
|---|---|---|
| 0 | 784555.555556 | 885.751407 |
MaxMember / MinMember¶
max_member and min_member search for the specified extremum of the given measure and return the member of the specified level for which the extremum is reached.
[10]:
m["MinMember of Price.SUM"] = tt.agg.min_member(m["Price.SUM"], lvl["City"])
m["MaxMember of Price.SUM"] = tt.agg.max_member(m["Price.SUM"], lvl["City"])
cube.query(m["MinMember of Price.SUM"], m["MaxMember of Price.SUM"])
[10]:
| MinMember of Price.SUM | MaxMember of Price.SUM | |
|---|---|---|
| 0 | HongKong | London |
No matter which level you execute the query on, the argmin is always performed at the level specified when defining the measure
[11]:
cube.query(
m["MinMember of Price.SUM"],
m["MaxMember of Price.SUM"],
levels=[lvl["Continent"], lvl["Country"]],
)
[11]:
| MinMember of Price.SUM | MaxMember of Price.SUM | ||
|---|---|---|---|
| Continent | Country | ||
| Asia | China | HongKong | Beijing |
| India | Dehli | Mumbai | |
| Europe | France | Lyon | Paris |
| UK | London | London |
Delete a measure¶
Any measure can be removed from the cube using del
[12]:
"Quantity running sum" in m
[12]:
True
[13]:
del m["Quantity running sum"]
"Quantity running sum" in m
[13]:
False
Different aggregations per level¶
It’s possible to aggregate a column differently depending on whether we are above or below a certain level.
For example, you can sum a quantity for each country and then take the average over all the countries:
[14]:
m["Average per country"] = tt.agg.mean(
m["Quantity.SUM"], scope=tt.scope.origin(lvl["Country"])
)
cube.query(m["Average per country"], levels=[lvl["Country"]])
[14]:
| Average per country | |
|---|---|
| Country | |
| China | 6000.0 |
| France | 7500.0 |
| India | 3700.0 |
| UK | 5500.0 |
[15]:
cube.query(m["Average per country"])
[15]:
| Average per country | |
|---|---|
| 0 | 5675.0 |
Calculated measures¶
Measures can be combined together to build more complex measures:
[16]:
m["Turnover"] = tt.agg.sum(m["Quantity.SUM"] * store["Price"])
cube.query(levels=[lvl["Country"]])
[16]:
| Average per country | Distinct City | MaxMember of Price.SUM | MinMember of Price.SUM | Price.MEAN | Price.SUM | Quantile 20 | Quantile 95 | Quantity standard deviation | Quantity variance | Quantity.LONG | Quantity.MAX | Quantity.MEAN | Quantity.MIN | Quantity.SHORT | Quantity.SUM | Turnover | contributors.COUNT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Country | ||||||||||||||||||
| China | 6000.0 | 2 | Beijing | HongKong | 380.0 | 760.0 | 2400.0 | 3900.0 | 1414.213562 | 2.000000e+06 | 6000.0 | 4000.0 | 3000.0 | 2000.0 | 0.0 | 6000.0 | 2220000.0 | 2 |
| France | 7500.0 | 3 | Paris | Lyon | 450.0 | 1800.0 | 1300.0 | 2850.0 | 853.912564 | 7.291667e+05 | 7500.0 | 3000.0 | 1875.0 | 1000.0 | 0.0 | 7500.0 | 3280000.0 | 4 |
| India | 3700.0 | 2 | Mumbai | Dehli | 380.0 | 760.0 | 1640.0 | 2165.0 | 494.974747 | 2.450000e+05 | 3700.0 | 2200.0 | 1850.0 | 1500.0 | 0.0 | 3700.0 | 1392000.0 | 2 |
| UK | 5500.0 | 1 | London | London | 480.0 | 960.0 | 2600.0 | 2975.0 | 353.553391 | 1.250000e+05 | 5500.0 | 3000.0 | 2750.0 | 2500.0 | 0.0 | 5500.0 | 2630000.0 | 2 |
Multidimensional Functions¶
Parent Value¶
[17]:
# Create multi-level hierarchy :
lvl = cube.levels
cube.hierarchies["Geography"] = {
"continent": lvl["Continent"],
"country": lvl["Country"],
"city": lvl["City"],
}
[18]:
help(tt.parent_value)
Help on function parent_value in module atoti._functions.multidimensional:
parent_value(measure: 'Union[Measure, str]', on: 'Hierarchy', *, apply_filters: 'bool' = False, degree: 'int' = 1, total_value: 'Optional[MeasureLike]' = None) -> 'Measure'
Return a measure equal to the passed measure at the parent member on the given hierarchy.
Example:
Measure definitions::
m1 = parent_value(Quantity.SUM, Date)
m2 = parent_value(Quantity.SUM, Date, degree=3)
m3 = parent_value(Quantity.SUM, Date, degree=3, total_value=Quantity.SUM))
m4 = parent_value(Quantity.SUM, Date, degree=3, total_value=Other.SUM))
Considering a non slicing hierarchy ``Date`` with three levels ``Years``, ``Month`` and ``Day``:
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| Year | Month | Day | Quantity.SUM | Other.SUM | m1 | m2 | m3 | m4 |
+============+=======+=====+==============+===========+=======+=======+=======+=======+
| 2019 | | | 75 | 1000 | 110 | null | 110 | 1500 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | 7 | | 35 | 750 | 75 | null | 110 | 1500 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 1 | 15 | 245 | 35 | 110 | 110 | 110 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 2 | 20 | 505 | 35 | 110 | 110 | 110 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | 6 | | 40 | 250 | 75 | null | 110 | 1500 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 1 | 25 | 115 | 40 | 110 | 110 | 110 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 2 | 15 | 135 | 40 | 110 | 110 | 110 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| 2018 | | | 35 | 500 | 110 | null | 110 | 1500 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | 7 | | 15 | 200 | 35 | null | 110 | 1500 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 1 | 5 | 55 | 15 | 110 | 110 | 110 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 2 | 10 | 145 | 15 | 110 | 110 | 110 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | 6 | | 20 | 300 | 35 | null | 110 | 1500 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 1 | 15 | 145 | 20 | 110 | 110 | 110 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 2 | 5 | 155 | 20 | 110 | 110 | 110 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
Considering a slicing hierarchy ``Date`` with three levels ``Years``, ``Month`` and ``Day``:
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| Year | Month | Day | Quantity.SUM | Other.SUM | m1 | m2 | m3 | m4 |
+============+=======+=====+==============+===========+=======+=======+=======+=======+
| 2019 | | | 75 | 1000 | 75 | null | 75 | 1000 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | 7 | | 35 | 750 | 75 | null | 75 | 1000 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 1 | 15 | 245 | 35 | 75 | 75 | 75 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 2 | 20 | 505 | 35 | 75 | 75 | 75 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | 6 | | 40 | 250 | 75 | null | 75 | 1000 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 1 | 25 | 115 | 40 | 75 | 75 | 75 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 2 | 15 | 135 | 40 | 75 | 75 | 75 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| 2018 | | | 35 | 500 | 35 | null | 35 | 500 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | 7 | | 15 | 200 | 35 | null | 35 | 500 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 1 | 5 | 55 | 15 | 35 | 35 | 35 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 2 | 10 | 145 | 15 | 35 | 35 | 35 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | 6 | | 20 | 300 | 35 | null | 35 | 500 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 1 | 15 | 145 | 20 | 35 | 35 | 35 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
| | | 2 | 5 | 155 | 20 | 35 | 35 | 35 |
+------------+-------+-----+--------------+-----------+-------+-------+-------+-------+
Args:
measure: The measure to take the parent value of.
on: The hierarchy to drill up to take the parent value.
apply_filters: Whether to apply the query filters when computing the
value at the parent member.
degree: The number of levels to go up to take the value on. A value
of ``1`` as parent_degree will do a one step drill up in the hierarchy.
total_value: The value to take when the drill up went above the top level of the hierarchy.
[19]:
m["Parent quantity"] = tt.parent_value(m["Quantity.SUM"], on=hier["Geography"])
We can check that the value on countries is equal to the Quantity.SUM on their continent :
[20]:
cube.query(m["Parent quantity"], levels=[lvl["continent"], lvl["country"]])
[20]:
| Parent quantity | ||
|---|---|---|
| continent | country | |
| Asia | China | 9700.0 |
| India | 9700.0 | |
| Europe | France | 13000.0 |
| UK | 13000.0 |
[21]:
cube.query(m["Quantity.SUM"], levels=[lvl["continent"]])
[21]:
| Quantity.SUM | |
|---|---|
| continent | |
| Asia | 9700.0 |
| Europe | 13000.0 |
Aggregate siblings¶
Siblings are all the children of the same member. For instance France and UK are children of Europe so France and UK are siblings.
[22]:
m["Sum siblings"] = tt.agg.sum(
m["Quantity.SUM"], scope=tt.scope.siblings(hier["Geography"])
)
cube.query(m["Sum siblings"], levels=[lvl["country"], lvl["city"]])
[22]:
| Sum siblings | |||
|---|---|---|---|
| continent | country | city | |
| Asia | China | Beijing | 6000.0 |
| HongKong | 6000.0 | ||
| India | Dehli | 3700.0 | |
| Mumbai | 3700.0 | ||
| Europe | France | Bordeaux | 7500.0 |
| Lyon | 7500.0 | ||
| Paris | 7500.0 | ||
| UK | London | 5500.0 |
[23]:
m["Average siblings"] = tt.agg.mean(
m["Quantity.SUM"], scope=tt.scope.siblings(hier["Geography"])
)
cube.query(m["Average siblings"], levels=[lvl["country"], lvl["city"]])
[23]:
| Average siblings | |||
|---|---|---|---|
| continent | country | city | |
| Asia | China | Beijing | 3000.0 |
| HongKong | 3000.0 | ||
| India | Dehli | 1850.0 | |
| Mumbai | 1850.0 | ||
| Europe | France | Bordeaux | 2500.0 |
| Lyon | 2500.0 | ||
| Paris | 2500.0 | ||
| UK | London | 5500.0 |
Shift¶
shift allows to get the value of previous or next members on a level
[24]:
m["next quantity"] = tt.shift(m["Quantity.SUM"], on=lvl["Date"], offset=1)
cube.query(m["next quantity"], levels=[lvl["Date"]])
[24]:
| next quantity | |
|---|---|
| Date | |
| 2018-01-01 | 8000.0 |
| 2019-01-01 | 4000.0 |
| 2019-01-02 | 7000.0 |
[25]:
cube.query(m["Quantity.SUM"], levels=[lvl["Date"]])
[25]:
| Quantity.SUM | |
|---|---|
| Date | |
| 2018-01-01 | 3700.0 |
| 2019-01-01 | 8000.0 |
| 2019-01-02 | 4000.0 |
| 2019-01-05 | 7000.0 |
Filter¶
filter allows you to only express the measure where certain conditions are met.filter. If you want to use conditions involving measures you should use where.You can combine conditions with the & bitwise operator.
[26]:
m["Filtered Quantity.SUM"] = tt.filter(
m["Quantity.SUM"], (lvl["City"] == "Paris") & (lvl["Color"] == "red")
)
cube.query(
m["Quantity.SUM"], m["Filtered Quantity.SUM"], levels=[lvl["Country"], lvl["Color"]]
)
[26]:
| Quantity.SUM | Filtered Quantity.SUM | ||
|---|---|---|---|
| Country | Color | ||
| China | blue | 2000.0 | NaN |
| green | 4000.0 | NaN | |
| France | blue | 4500.0 | NaN |
| red | 3000.0 | 1000.0 | |
| India | blue | 1500.0 | NaN |
| red | 2200.0 | NaN | |
| UK | green | 3000.0 | NaN |
| red | 2500.0 | NaN |
Where¶
where defines an if-then-else measure whose value depends on certain conditions. It is similar to numpy’s where function.
[27]:
# Label large amounts
m["Large quantities"] = tt.where(m["Quantity.SUM"] >= 3000, "large", "small")
# Double up UK's quantities
m["Double UK"] = tt.where(
lvl["Country"] == "UK", 2 * m["Quantity.SUM"], m["Quantity.SUM"]
)
cube.query(
m["Quantity.SUM"],
m["Large quantities"],
m["Double UK"],
levels=[lvl["Country"], lvl["Color"]],
)
[27]:
| Quantity.SUM | Large quantities | Double UK | ||
|---|---|---|---|---|
| Country | Color | |||
| China | blue | 2000.0 | small | 2000.0 |
| green | 4000.0 | large | 4000.0 | |
| France | blue | 4500.0 | large | 4500.0 |
| red | 3000.0 | large | 3000.0 | |
| India | blue | 1500.0 | small | 1500.0 |
| red | 2200.0 | small | 2200.0 | |
| UK | green | 3000.0 | large | 6000.0 |
| red | 2500.0 | small | 5000.0 |
At¶
at takes the value of the given measure shifted on one of the level to the given value.
The value can be a literal value or the value of another level
[28]:
m["Blue Quantity"] = tt.at(m["Quantity.SUM"], {lvl["Color"]: "blue"})
cube.query(m["Quantity.SUM"], m["Blue Quantity"], levels=[lvl["Color"]])
[28]:
| Quantity.SUM | Blue Quantity | |
|---|---|---|
| Color | ||
| blue | 8000.0 | 8000.0 |
| green | 7000.0 | 8000.0 |
| red | 7700.0 | 8000.0 |
The measure is null if the level is not expressed
[29]:
cube.query(m["Quantity.SUM"], m["Blue Quantity"])
[29]:
| Quantity.SUM | Blue Quantity | |
|---|---|---|
| 0 | 22700.0 | None |
In a multilevel hierarchy, only the shifted level is changed. For instance if we shift the country to “France”, [Europe, UK] is shifted to [Europe,France] and [Asia,China] is shifted to [Asia,France] which does not exist.
[30]:
m["France Quantity Fail"] = tt.at(m["Quantity.SUM"], {lvl["country"]: "France"})
cube.query(
m["Quantity.SUM"],
m["France Quantity Fail"],
levels=[lvl["continent"], lvl["country"]],
)
[30]:
| Quantity.SUM | France Quantity Fail | ||
|---|---|---|---|
| continent | country | ||
| Asia | China | 6000.0 | NaN |
| India | 3700.0 | NaN | |
| Europe | France | 7500.0 | 7500.0 |
| UK | 5500.0 | 7500.0 |
The expected value can be obtained by shifting both levels to the requested values as follow.
[31]:
m["France Quantity"] = tt.at(
m["Quantity.SUM"], {lvl["country"]: "France", lvl["continent"]: "Europe"}
)
cube.query(
m["Quantity.SUM"], m["France Quantity"], levels=[lvl["continent"], lvl["country"]]
)
[31]:
| Quantity.SUM | France Quantity | ||
|---|---|---|---|
| continent | country | ||
| Asia | China | 6000.0 | 7500.0 |
| India | 3700.0 | 7500.0 | |
| Europe | France | 7500.0 | 7500.0 |
| UK | 5500.0 | 7500.0 |
Other Functions¶
Mathematical functions¶
round, floor, and ceil: closest, lower, and upper rounding of double values
[32]:
m["round"] = tt.round(m["Quantity.SUM"] / 1000) * 1000
m["floor"] = tt.floor(m["Quantity.SUM"] / 1000) * 1000
m["ceil"] = tt.ceil(m["Quantity.SUM"] / 1000) * 1000
cube.query(
m["Quantity.SUM"], m["floor"], m["ceil"], m["round"], levels=[lvl["Country"]]
)
[32]:
| Quantity.SUM | floor | ceil | round | |
|---|---|---|---|---|
| Country | ||||
| China | 6000.0 | 6000 | 6000 | 6000 |
| France | 7500.0 | 7000 | 8000 | 8000 |
| India | 3700.0 | 3000 | 4000 | 4000 |
| UK | 5500.0 | 5000 | 6000 | 6000 |
exp: Exponential is Euler’s number e raised to the power of a double value.
[33]:
m["Zero"] = 0.0
m["One"] = tt.exp(m["Zero"])
log: the natural (base e) logarithm
[34]:
m["Log Quantity"] = tt.log(m["Quantity.SUM"])
cube.query(m["Log Quantity"], levels=[lvl["Country"]])
[34]:
| Log Quantity | |
|---|---|
| Country | |
| China | 8.699515 |
| France | 8.922658 |
| India | 8.216088 |
| UK | 8.612503 |
log10: the base 10 logarithm
[35]:
m["Log10 Quantity"] = tt.log10(m["Quantity.SUM"])
cube.query(m["Log10 Quantity"], levels=[lvl["Country"]])
[35]:
| Log10 Quantity | |
|---|---|
| Country | |
| China | 3.778151 |
| France | 3.875061 |
| India | 3.568202 |
| UK | 3.740363 |
abs: the absolute value of a given measure
[36]:
m["Negative"] = -1 * m["Quantity.SUM"]
m["abs"] = tt.abs(m["Negative"])
cube.query(m["abs"])
[36]:
| abs | |
|---|---|
| 0 | 22700.0 |
sin: the sinus value of a given measure
[37]:
m["Sinus Quantity"] = tt.sin(m["Quantity.SUM"])
cube.query(m["Sinus Quantity"], levels=[lvl["Country"]])
[37]:
| Sinus Quantity | |
|---|---|
| Country | |
| China | -0.427720 |
| France | -0.851236 |
| India | -0.714666 |
| UK | 0.800864 |
cos: the cosinus value of a given measure
[38]:
m["Cosinus Quantity"] = tt.cos(m["Quantity.SUM"])
cube.query(m["Cosinus Quantity"], levels=[lvl["Country"]])
[38]:
| Cosinus Quantity | |
|---|---|
| Country | |
| China | 0.903912 |
| France | -0.524783 |
| India | 0.699466 |
| UK | -0.598846 |
tan: the tangent value of a given measure
[39]:
m["Tangent Quantity"] = tt.tan(m["Quantity.SUM"])
cube.query(m["Tangent Quantity"], levels=[lvl["Country"]])
[39]:
| Tangent Quantity | |
|---|---|
| Country | |
| China | -0.473187 |
| France | 1.622071 |
| India | -1.021730 |
| UK | -1.337344 |
pow: the calculated power value of a given measure
[40]:
m["Power int Quantity"] = m["Quantity.SUM"] ** 2
cube.query(m["Power int Quantity"], levels=[lvl["Country"]])
[40]:
| Power int Quantity | |
|---|---|
| Country | |
| China | 36000000.0 |
| France | 56250000.0 |
| India | 13690000.0 |
| UK | 30250000.0 |
[41]:
m["Power float Quantity"] = m["Quantity.SUM"] ** 0.5
cube.query(m["Power float Quantity"], levels=[lvl["Country"]])
[41]:
| Power float Quantity | |
|---|---|
| Country | |
| China | 77.459667 |
| France | 86.602540 |
| India | 60.827625 |
| UK | 74.161985 |
[42]:
m["Power measure Quantity"] = m["Quantity.SUM"] ** m["Quantity.SUM"]
cube.query(m["Power measure Quantity"], levels=[lvl["Country"]])
[42]:
| Power measure Quantity | |
|---|---|
| Country | |
| China | Infinity |
| France | Infinity |
| India | Infinity |
| UK | Infinity |
[43]:
m["Power neg Quantity"] = m["Quantity.SUM"] ** -3
cube.query(m["Power neg Quantity"], levels=[lvl["Country"]])
[43]:
| Power neg Quantity | |
|---|---|
| Country | |
| China | 4.629630e-12 |
| France | 2.370370e-12 |
| India | 1.974217e-11 |
| UK | 6.010518e-12 |
sqrt: the square root value of a given measure
[44]:
m["Sqrt Quantity"] = tt.sqrt(m["Quantity.SUM"])
cube.query(m["Sqrt Quantity"], levels=[lvl["Country"]])
[44]:
| Sqrt Quantity | |
|---|---|
| Country | |
| China | 77.459667 |
| France | 86.602540 |
| India | 60.827625 |
| UK | 74.161985 |
Time functions¶
date_diff is the number of days between 2 dates:
[45]:
from datetime import datetime
lvl = cube.levels
m["Days from today"] = tt.date_diff(datetime.now().date(), lvl["Date"])
cube.query(m["Days from today"], levels=[lvl["Date"]])
[45]:
| Days from today | |
|---|---|
| Date | |
| 2018-01-01 | -875 |
| 2019-01-01 | -510 |
| 2019-01-02 | -509 |
| 2019-01-05 | -506 |
Measure Folder¶
Measures can be put into folders to group them in the UI.
[46]:
for name in [
"Quantity.SUM",
"Quantity.MEAN",
"Quantity.LONG",
"Quantity.MAX",
"Quantity.MIN",
"Quantity.SHORT",
]:
m[name].folder = "Quantity"
[47]:
m["Quantity.SUM"].folder
[47]:
'Quantity'
Measure formatter¶
Measures have formatters describing how to represent them as strings. These formatters can be modified in Python or directly in the UI. Here are a few examples of what is possible, more documentation on how to write an MDX formatter can be found on docs.microsoft.com.
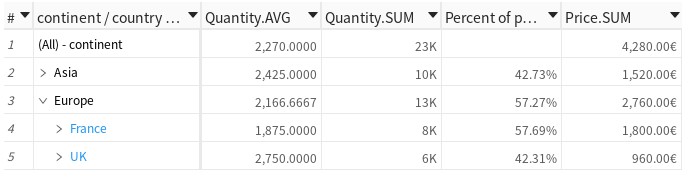
[48]:
# Convert to thousands
m["Quantity.SUM"].formatter = "DOUBLE[#,###,K]"
# Add a unit
m["Price.SUM"].formatter = "DOUBLE[#,###.00€]"
# Add more decimal figures
m["Quantity.MEAN"].formatter = "DOUBLE[#,###.0000]"
# Display as percent
m["Percent of parent"] = m["Quantity.SUM"] / m["Parent quantity"]
m["Percent of parent"].formatter = "DOUBLE[#,###.00%]"